图

huan_kong

900字约3分钟

2024-05-08

介绍

一组顶点:
- 通常用 V (Vertex) 表示顶点的集合
一组边：通常用 E (Edge) 表示边的集合
- 边是顶点和顶点之间的连线
- 边可以是有向的, 也可以是无向的
  - 比如 A --- B, 通常表示无向
  - 比如 A --> B, 通常表示有向

术语

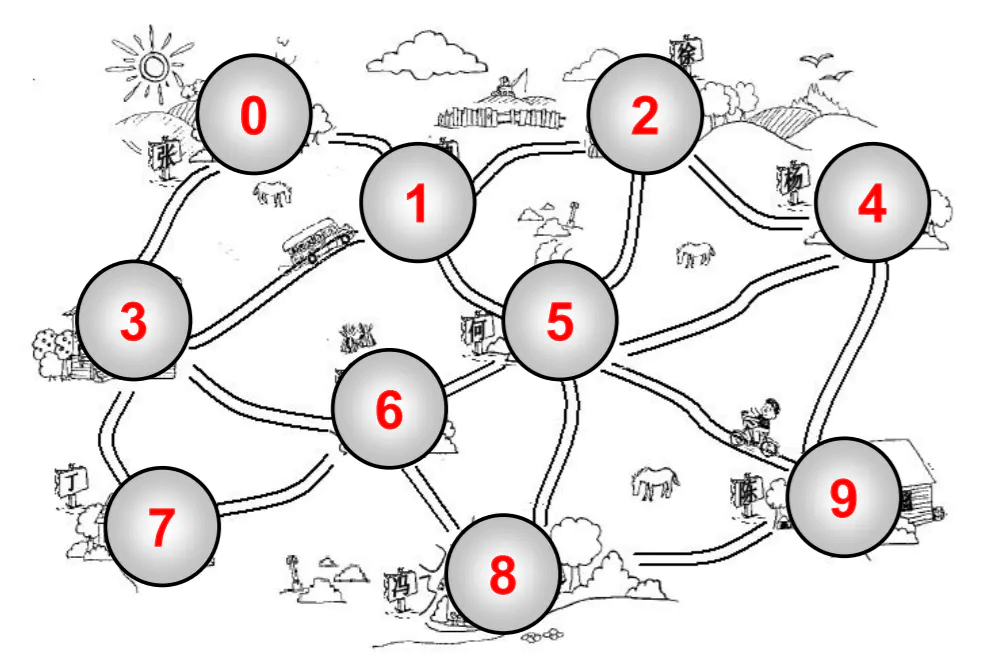
顶点
- 顶点表示图中的一个节点.
- 比如地铁站中某个站/多个村庄中的某个村庄/互联网中的某台主机/人际关系中的人.
边
- 边表示顶点和顶点之间的连线.
- 比如地铁站中两个站点之间的直接连线, 就是一个边.
- 注意：这里的边不要叫做路径, 路径有其他的概念, 后面会区分.
相邻顶点
- 由一条边连接在一起的顶点称为相邻顶点.
- 比如 0 - 1 是相邻的, 0 - 3 是相邻的. 0 - 2 是不相邻的.
度
- 一个顶点的度是相邻顶点的数量
- 比如 0 顶点和其他两个顶点相连, 0 顶点的度是 2
- 比如 1 顶点和其他四个顶点相连, 1 顶点的度是 4
路径
- 路径是顶点 v1, v2..., vn 的一个连续序列, 比如上图中 0 1 5 9 就是一条路径.
- 简单路径：简单路径要求不包含重复的顶点. 比如 0 1 5 9 是一条简单路径.
- 回路：第一个顶点和最后一个顶点相同的路径称为回路. 比如 0 1 5 6 3 0.
无向图
- 上面的图就是一张无向图, 因为所有的边都没有方向.
- 比如 0 - 1 之间有边, 那么说明这条边可以保证 0 -> 1, 也可以保证 1 -> 0.
有向图
- 有向图表示的图中的边是有方向的.
- 比如 0 -> 1, 不能保证一定可以 1 -> 0, 要根据方向来定.
无权图
- 如上图就是一张无权图, 边没有携带权重.
- 上图中的边是没有任何意义的, 不能说 0 - 1 的边, 比 4 - 9 的边更远或者用的时间更长.
带权图
- 带权图表示边有一定的权重
- 这里的权重可以是任意你希望表示的数据：比如距离或者花费的时间或者票价.
- 我们来看一张有向和带权的图：

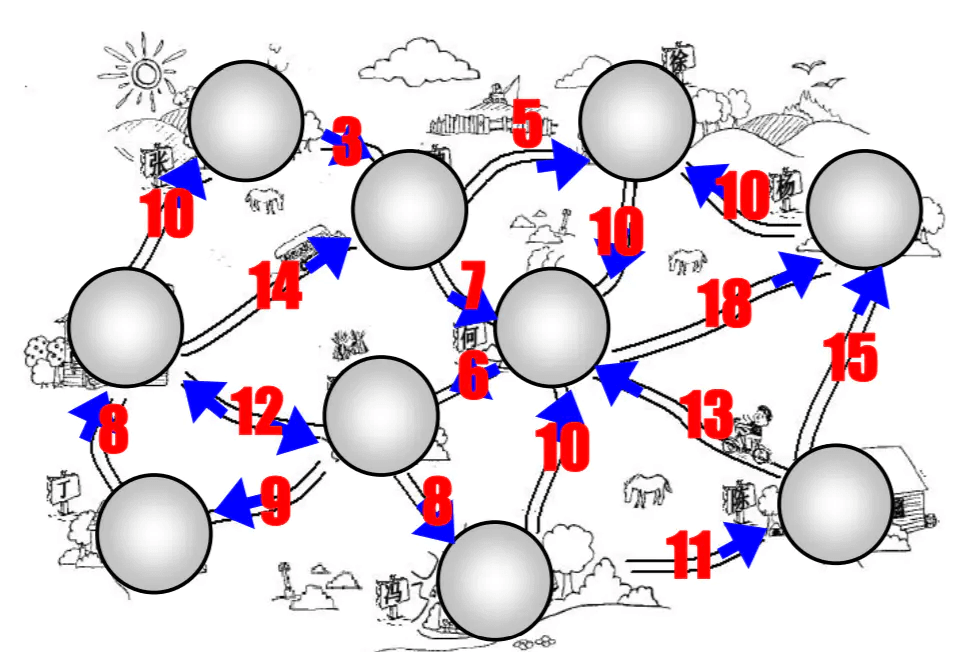
表示方法

邻接矩阵

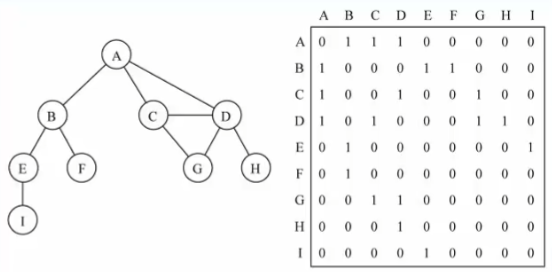
我们可以制定一个规则, 0表示他们没有链接, 1表示他们有链接

如果这里需要权重, 那么0的意思不变, 后面别的数字就可以是他们的权重

不过这种方法有些浪费空间, 存在大量0

邻接表

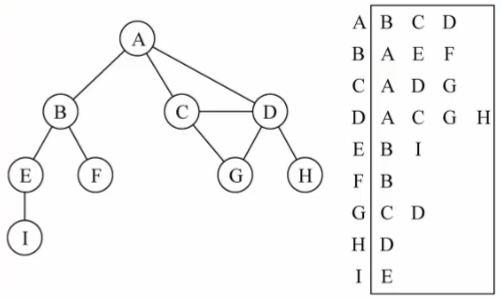
类似哈希表的存储方式

获取链接到了谁很容易, 但是如果想需要获取谁链接了自己很难, 可以使用逆邻接表

遍历方法

都需要指明第一个被访问的顶点

广度优先搜索 Breadth-First Search(BFS)

把当前节点的所有分支全部走一遍, 然后再重新到分支的节点, 把他的所有分支都再走一遍

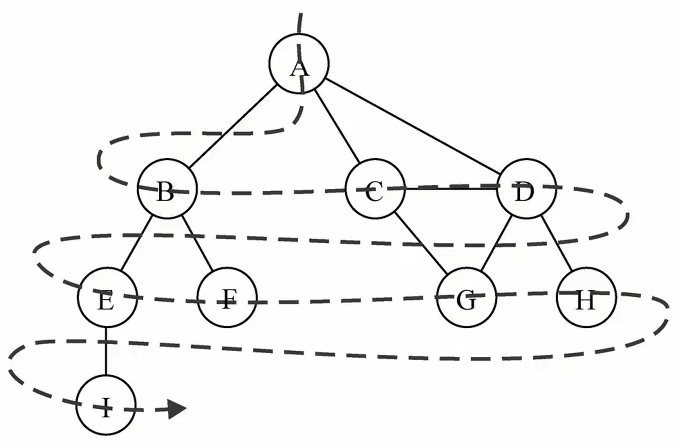
深度优先搜索 Depth-First Search(DFS)

一条路走到底, 走到底然后开始往回看, 检查前面节点的别的分支是否都已经经过

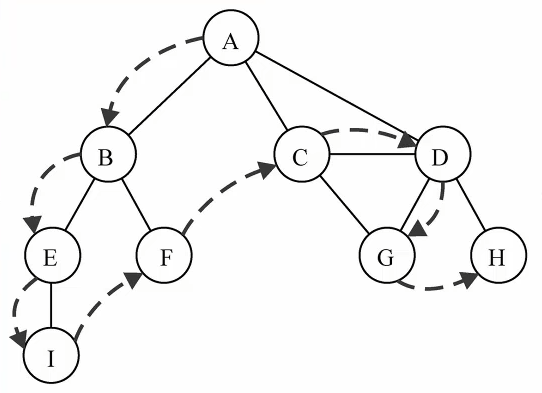
TS实现

namespace 图 {
  class Dictionay<T> {
    #values: { [key: string]: T } = {}

    has(key: string) {
      return this.#values.hasOwnProperty(key)
    }

    set(key: string, value: T) {
      this.#values[key] = value
    }

    remove(key: string) {
      if (!this.has(key)) return false
      delete this.#values[key]
    }

    get(key: string) {
      return this.has(key) ? this.#values[key] : undefined
    }

    keys() {
      return Object.keys(this.#values)
    }

    values() {
      return Object.values(this.#values)
    }

    size() {
      return this.keys().length
    }

    clear() {
      this.#values = {}
    }
  }

  class Queue<T> {
    #value: T[] = []

    enqueue(element: T) {
      return this.#value.push(element)
    }

    dequeue() {
      return this.#value.shift()
    }

    front() {
      return this.#value[0]
    }

    isEmpty() {
      return this.#value.length === 0
    }

    size() {
      return this.#value.length
    }

    toString() {
      return this.#value.toString()
    }
  }

  interface color {
    [key: string]: 'white' | 'gray' | 'black'
  }

  type func = (value: string) => void

  class Graph {
    // 顶点
    #vertexes: string[] = []
    #edges: Dictionay<string[]> = new Dictionay()

    constructor() {}

    addVertex(vertex: string) {
      if (this.#vertexes.includes(vertex)) return
      this.#vertexes.push(vertex)
      this.#edges.set(vertex, [])
    }

    addEdge(vertex1: string, vertex2: string) {
      if (!this.#edges.has(vertex1) || !this.#edges.has(vertex2)) return
      this.#edges.get(vertex1)!.push(vertex2)
      this.#edges.get(vertex2)!.push(vertex1)
    }

    toString() {
      return this.#vertexes
        .map((vertex) => `${vertex} => ${this.#edges.get(vertex)?.join(' ')}`)
        .join('\n')
    }

    initColor(): color {
      /**
       * @description 白色: 没有被访问过
       * @description 灰色: 被访问过, 但没有完成探索
       * @description 黑色: 被访问过, 并且探索完成
       */
      return this.#vertexes.reduce((previousValue, currentValue) => {
        previousValue[currentValue] = 'white'
        return previousValue
      }, {})
    }

    // 广度优先搜索算法
    BFS(initVertexes: string, func: func) {
      const queue = new Queue<string>()
      const color = this.initColor()

      queue.enqueue(initVertexes)
      while (!queue.isEmpty()) {
        // 取出顶点
        const currentVertex = queue.dequeue() as string

        // 获取相连的其余顶点
        const edges = this.#edges.get(currentVertex) as string[]

        // 设置为灰色
        color[initVertexes] = 'gray'

        // 遍历所有边, 添加到队列中
        edges.forEach((edge) => {
          // 如果是白色, 则设置为灰色, 并添加到队列中
          // 如果是灰色, 则跳过, 因为已经被访问过了
          if (color[edge] === 'white') {
            color[edge] = 'gray'
            queue.enqueue(edge)
          }
        })

        func(currentVertex)

        color[initVertexes] = 'black'
      }
    }

    // 深度优先搜索算法(队列方法)
    DFSQueue(initVertexes: string, func: func) {
      const queue = new Queue<string>()
      const color = this.initColor()

      queue.enqueue(initVertexes)
      while (!queue.isEmpty()) {
        // 取出顶点
        const currentVertex = queue.dequeue() as string

        // 获取相连的其余顶点
        const edges = this.#edges.get(currentVertex) as string[]

        // 设置为灰色
        color[initVertexes] = 'gray'

        // 遍历所有边, 添加到队列中
        edges.forEach((edge) => {
          // 如果是白色, 则设置为灰色, 并添加到队列中
          if (color[edge] === 'white') {
            color[edge] = 'gray'
            queue.enqueue(edge)
          }
        })

        func(currentVertex)

        color[initVertexes] = 'black'
      }
    }

    // 深度优先搜索算法(递归方法)
    DFS(initVertexes: string, func: func) {
      const color = this.initColor()
      this.DFSVisit(initVertexes, color, func)
    }

    DFSVisit(vertexes: string, color: color, func: func) {
      color[vertexes] = 'gray'

      // 获取相连的其余顶点
      const edges = this.#edges.get(vertexes) as string[]

      // 设置为灰色
      color[vertexes] = 'gray'

      func(vertexes)

      // 遍历所有边
      edges.forEach((edge) => {
        // 如果是白色, 则设置为灰色, 并开始递归调用
        if (color[edge] === 'white') {
          color[edge] = 'gray'
          this.DFSVisit(edge, color, func)
        }
      })

      color[vertexes] = 'black'
    }
  }
}