介绍

Binary Search Tree 缩写 BST, 又称为 二叉排序树/二叉查询树

二叉搜索树是一颗二叉树，可为空

如果不为空，满足以下性质:

• 非空左子树的所有键值小于其根节点的键值
• 非空右子树的所有键值大于其根节点的键值
• 左，右子树本身也都是二叉搜索树

特点

• 小的值在左，大的值在右

TS 实现

/* eslint-disable unused-imports/no-unused-vars */
class BinarySearchTreeNode<T> {
  #key: number
  #value: T
  #left: BinarySearchTreeNode<T> | null
  #right: BinarySearchTreeNode<T> | null

  constructor(key: number, value: T) {
    this.#key = key
    this.#value = value
    this.#left = null
    this.#right = null
  }

  getKey() {
    return this.#key
  }

  getValue() {
    return this.#value
  }

  getLeft() {
    return this.#left
  }

  getRight() {
    return this.#right
  }

  setLeft(left: BinarySearchTreeNode<T> | null): boolean {
    this.#left = left
    return true
  }

  setRight(right: BinarySearchTreeNode<T> | null): boolean {
    this.#right = right
    return true
  }
}

type BinarySearchResult<T> = [true, BinarySearchTreeNode<T>] | [false, null]

class BinarySearchTree<T = any> {
  #root: BinarySearchTreeNode<T> | null = null

  insert(key: number, value: T): boolean {
    const node = new BinarySearchTreeNode(key, value)

    if (!this.#root) {
      this.#root = node
      return true
    }

    this.#insertNode(this.#root, node)

    return true
  }

  #insertNode(node: BinarySearchTreeNode<T>, newNode: BinarySearchTreeNode<T>): boolean {
    if (newNode.getKey() < node.getKey()) {
      // 小于当前节点，插入左子树
      const nodeLeft = node.getLeft()
      if (nodeLeft === null) {
        node.setLeft(newNode)
        return true
      }
      else {
        return this.#insertNode(nodeLeft, newNode)
      }
    }
    else {
      // 大于等于当前节点，插入右子树
      const nodeRight = node.getRight()
      if (nodeRight === null) {
        node.setRight(newNode)
        return true
      }
      else {
        return this.#insertNode(nodeRight, newNode)
      }
    }
  }

  // search(key: number): BinarySearchResult<T> {

  // }

  preOrderTraversal(key: number): BinarySearchResult<T> {
    return this.#preOrderTraversalNode(this.#root, key)
  }

  #preOrderTraversalNode(node: BinarySearchTreeNode<T> | null, key: number): BinarySearchResult<T> {
    if (node === null) {
      return [false, null]
    }
    else if (node.getKey() === key) {
      return [true, node]
    }

    const left = this.#preOrderTraversalNode(node.getLeft(), key)
    if (left[0]) {
      return left
    }

    return this.#preOrderTraversalNode(node.getRight(), key)
  }

  inOrderTraversal(key: number): BinarySearchResult<T> {
    return this.#inOrderTraversalNode(this.#root, key)
  }

  #inOrderTraversalNode(node: BinarySearchTreeNode<T> | null, key: number): BinarySearchResult<T> {
    if (node === null) {
      return [false, null]
    }

    const left = this.#inOrderTraversalNode(node.getLeft(), key)
    if (left[0]) {
      return left
    }

    if (node.getKey() === key) {
      return [true, node]
    }

    return this.#inOrderTraversalNode(node.getRight(), key)
  }

  postOrderTraversal(key: number): BinarySearchResult<T> {
    return this.#postOrderTraversalNode(this.#root, key)
  }

  #postOrderTraversalNode(node: BinarySearchTreeNode<T> | null, key: number): BinarySearchResult<T> {
    if (node === null) {
      return [false, null]
    }

    const left = this.#postOrderTraversalNode(node.getLeft(), key)
    if (left[0]) {
      return left
    }

    const right = this.#postOrderTraversalNode(node.getRight(), key)
    if (right[0]) {
      return right
    }

    if (node.getKey() === key) {
      return [true, node]
    }

    return [false, null]
  }

  min() { }

  max() { }

  remove(key: number) { }

  // // 先序遍历
  // preOrderTraversal(handler: (node: BinarySearchTreeNode) => any) {
  //   this.#preOrderTraversalNode(this.#root, handler)
  // }

  // #preOrderTraversalNode(node: BinarySearchTreeNode | null, handler: (node: BinarySearchTreeNode) => any) {
  //   if (node === null)
  //     return
  //   handler(node)
  //   this.#preOrderTraversalNode(node.getLeft(), handler)
  //   this.#preOrderTraversalNode(node.getRight(), handler)
  // }

  // // 中序遍历
  // inOrderTraversal(handler: (node: BinarySearchTreeNode) => any) {
  //   this.#inOrderTraversalNode(this.#root, handler)
  // }

  // #inOrderTraversalNode(node: BinarySearchTreeNode | null, handler: (node: BinarySearchTreeNode) => any) {
  //   if (node === null)
  //     return
  //   this.#inOrderTraversalNode(node.getLeft(), handler)
  //   handler(node)
  //   this.#inOrderTraversalNode(node.getRight(), handler)
  // }

  // // 后序遍历
  // postOrderTraversal(handler: (node: BinarySearchTreeNode) => any) {
  //   this.#postOrderTraversalNode(this.#root, handler)
  // }

  // #postOrderTraversalNode(node: BinarySearchTreeNode | null, handler: (node: BinarySearchTreeNode) => any) {
  //   if (node === null)
  //     return
  //   this.#postOrderTraversalNode(node.getLeft(), handler)
  //   this.#postOrderTraversalNode(node.getRight(), handler)
  //   handler(node)
  // }

  // min() {
  //   let node = this.#root
  //   if (node === null)
  //     return node
  //   let left = node.getLeft()
  //   while (left !== null) {
  //     node = left
  //     left = node.getLeft()
  //   }
  //   return node.getKey()
  // }

  // max() {
  //   let node = this.#root
  //   if (node === null)
  //     return node
  //   let right = node.getRight()
  //   while (right !== null) {
  //     node = right
  //     right = node.getRight()
  //   }
  //   return node.getKey()
  // }

  // search(key: number) {
  //   return this.#searchNode(this.#root, key)
  // }

  // #searchNode(node: BinarySearchTreeNode | null, key: number) {
  //   if (node === null)
  //     return false

  //   if (key < node.getKey()) {
  //     return this.#searchNode(node.getLeft(), key)
  //   }
  //   else if (key > node.getKey()) {
  //     return this.#searchNode(node.getRight(), key)
  //   }
  //   else {
  //     return node
  //   }
  // }

  // search2(key: number) {
  //   let node = this.#root
  //   let nowKey: number | null = null

  //   while (node !== null) {
  //     nowKey = node.getKey()
  //     if (key < nowKey) {
  //       node = node.getLeft()
  //     }
  //     else if (key > nowKey) {
  //       node = node.getRight()
  //     }
  //     else {
  //       return node
  //     }
  //   }

  //   return false
  // }

  // remove(key: number) {
  //   if (this.#root === null)
  //     return this.#root
  //   let current: BinarySearchTreeNode | null = this.#root
  //   const rootKey = this.#root.getKey()
  //   let parent: BinarySearchTreeNode | null = null
  //   let isLeftChild = true

  //   const currentKey = current.getKey()
  //   while (currentKey !== key) {
  //     parent = current
  //     if (key < currentKey) {
  //       isLeftChild = true
  //       current = current.getLeft()
  //     }
  //     else {
  //       isLeftChild = false
  //       current = current.getRight()
  //     }

  //     if (current === null)
  //       return false
  //   }

  //   if (current.getLeft() === null && current.getRight() === null) {
  //     // 如果没有子节点
  //     if (currentKey === rootKey) {
  //       this.#root = null
  //     }
  //     else if (isLeftChild) {
  //       if (parent === null)
  //         return parent
  //       parent.setLeft(null)
  //     }
  //     else {
  //       if (parent === null)
  //         return parent
  //       parent.setRight(null)
  //     }
  //   }
  //   else if (current.getLeft() === null) {
  //     // 如果没有左子节点
  //     if (current.getKey() === rootKey) {
  //       this.#root = current.getRight()
  //     }
  //     else if (isLeftChild) {
  //       if (parent === null)
  //         return parent
  //       parent.setLeft(current.getRight())
  //     }
  //     else {
  //       if (parent === null)
  //         return parent
  //       parent.setRight(current.getRight())
  //     }
  //   }
  //   else if (current.getRight() === null) {
  //     // 如果没有右子节点
  //     if (current.getKey() === rootKey) {
  //       this.#root = current.getLeft()
  //     }
  //     else if (isLeftChild) {
  //       if (parent === null)
  //         return parent
  //       parent.setLeft(current.getLeft())
  //     }
  //     else {
  //       if (parent === null)
  //         return parent
  //       parent.setRight(current.getLeft())
  //     }
  //   }
  //   else {
  //     // 如果有右还有右子节点
  //     const successor = this.getSuccessor(current)

  //     if (currentKey === rootKey) {
  //       this.#root = successor
  //     }
  //     else if (isLeftChild) {
  //       if (parent === null)
  //         return parent
  //       parent.setLeft(successor)
  //     }
  //     else {
  //       if (parent === null)
  //         return parent
  //       parent.setRight(successor)
  //     }

  //     if (successor === null)
  //       return successor

  //     successor.setLeft(current.getLeft())
  //   }
  //   return true
  // }

  // getSuccessor(delNode: BinarySearchTreeNode) {
  //   let successorParent: BinarySearchTreeNode | null = delNode
  //   let successor = delNode.getRight()
  //   let current = delNode.getRight()

  //   while (current !== null) {
  //     successorParent = successor
  //     successor = current
  //     current = current.getLeft()
  //   }

  //   if (successor !== delNode.getRight()) {
  //     if (successorParent === null || successor === null)
  //       return successor
  //     successorParent.setLeft(successor.getRight())
  //     successor.setRight(delNode.getRight())
  //   }
  //   return successor
  // }
}

实现原理

遍历数据

这里所说的树的遍历不仅仅针对二叉搜索树，而是适用于所有的二叉树.

常见的三种二叉树遍历方式为:

• 先序遍历
• 中序遍历
• 后序遍历

先序遍历

首先，遍历根节点，然后，遍历其左子树，最后，遍历其右子树

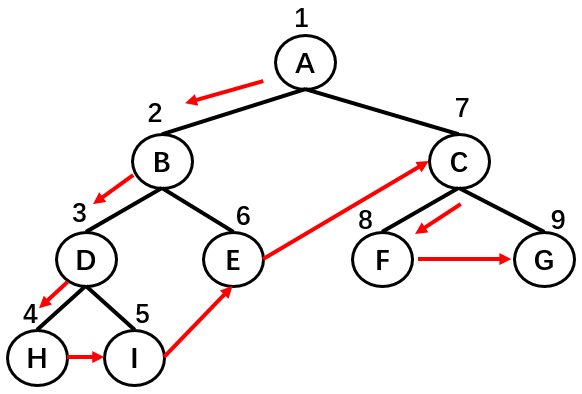
如上图所示，二叉树的节点遍历顺序为: A -> B -> D -> H -> I -> E -> C -> F -> G

中序遍历

首先，遍历其左子树，然后，遍历根 ( 父 ) 节点，最后，遍历其右子树

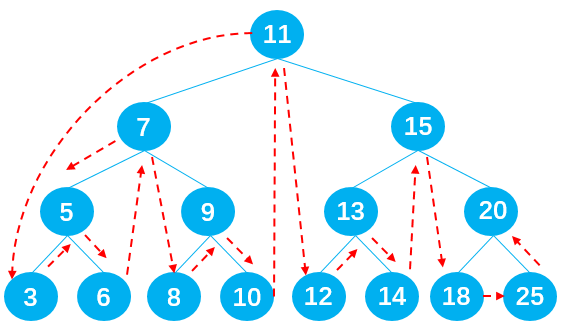
输出节点的顺序应为: 3 -> 5 -> 6 -> 7 -> 8 -> 9 -> 10 -> 11 -> 12 -> 13 -> 14 -> 15 -> 18 -> 20 -> 25

后序遍历

首先，遍历其左子树，然后，遍历其右子树，最后，遍历根 ( 父 ) 节点

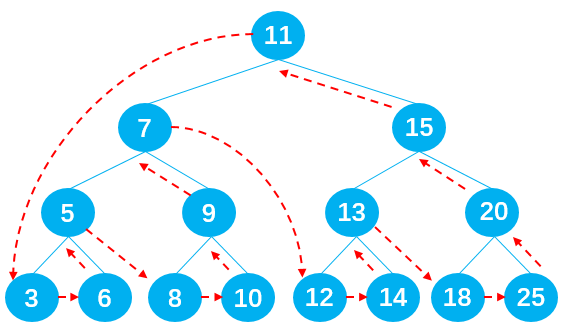
输出节点的顺序应为: 3 -> 6 -> 5 -> 8 -> 10 -> 9 -> 7 -> 12 -> 14 -> 13 -> 18 -> 25 -> 20 -> 15 -> 11

编辑此页

上一页二叉树

下一页红黑树